- SNR is a ratio of two measurements, level and noise measurements, expressed in dB.
- Signal level, measurement bandwidth, and weighting filter must be defined.
- Dynamic range is like SNR but noise is measured in the presence of small signal; results should be the same.
Noise is one of the most important performance figures and typically given as SNR, Signal-to-Noise Ratio. This is a ratio of two separate measurements: high/maximum signal level and noise level without signal. In audio measurements, signals and noise are typically expressed in level instead of power. Thus,
SNR(dB) = 20*log10(signal_level/noise_level).
It is important that both levels are expressed with the same unit. As amplitude or peak value definition for noise is cumbersome, RMS values are typically used.
“SNR of H-DAC is 122 dB” – what does this mean and what else should be known?
As SNR is a ratio of signal level and noise level, 122 dB means that noise floor is 10^(122/20) = 1.26 million times lower than the signal level. That is a big number – that is why we use decibels.
Regarding measurement, we need to know and understand following conditions.
Signal level
Besides signal level we are interested in the amount of distortion at that level, especially in analog devices. One can make SNR look better by driving large heavily distorted signal, thus getting higher signal level and higher SNR although it does not reflect real conditions (which unfortunately is common when performance figures are obtained for marketing purposes).
In DACs the level is typically maximum signal level, denoted as 0 dBFS (dB to full-scale), just remember that dBFS is different unit and cannot be used when deriving SNR – analog voltage must be known as well.
Signal frequency can be mentioned as well but it does not have effect on the measurement. It is a “middle frequency” tone, typically 1 kHz.
Measurement bandwidth
Noise in these systems is white noise, meaning its power spectral density is flat. Therefore, noise power is proportional to bandwidth and, theoretically, if we had infinite bandwidth we would have infinite power. In practice, with white noise only, doubling the bandwidth doubles the noise, meaning 3 dB rise. Therefore, for the best SNR number we want to use as small bandwidth as possible. Typically this is the common audio bandwidth 20 Hz – 20 kHz, and we can assume that if it is not given.
Weighting
A-weighting is often used for noise values to give more weight to frequencies where human hearing is more sensitive. When white noise spectrum is flat, this means lowering the effect of low and high frequencies. A-weighting filter lowers the noise floor (improves the SNR) by 2-3 dB. It is often used in SNR measurements, and you can assume it is used even if it is not mentioned.
Overall, when not enough measurement conditions are given, good rule of thumb is to assume the conditions that make the figures the best.
Spectral examples
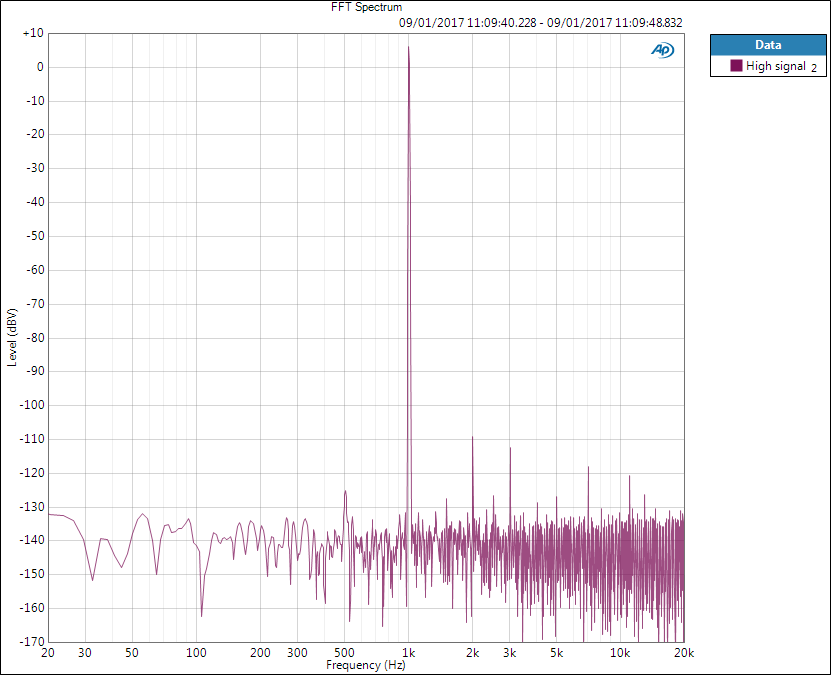
Below are some illustrations with FFT images. First is an image with 6 dBV (2 Vrms) 1 kHz signal, let’s say this is the maximum level of our system.
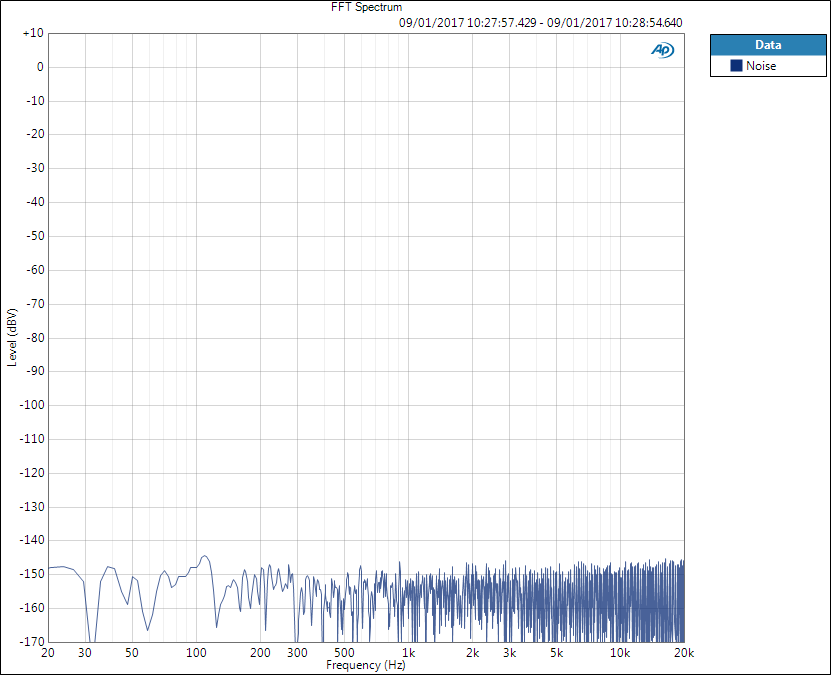
Next image is noise only and its level (RMS level in the 20 Hz – 20 kHz bandwidth) here is -119 dBV (this is the noise floor of APx585, by the way).
Note that noise level is not -150 dBV as it seems on the FFT. The value seen belongs to one very narrow FFT bin and its value depends on the bin size and window function. This is due to scaling to show discrete tone levels correctly (see AP: FFT scaling for noise). Noise level can be derived by correcting this scaling and integrating over the measurement bandwidth, typically 20 Hz – 20 kHz. Therefore, while we can see the level of sine tones directly at y-axis, we cannot see the noise level. However, when noise level is measured, we simply use RMS level meter and bandwidth limiting filters; there is no need to know all the details.
Now SNR would be the ratio of these two numbers: 6 dBV and -119 dBV – that is 125 dB. This is a non-weighted value so to please the marketing department we would use weighting filter to get 2-3 dB more – because everyone else does that as well.
Note that noise floor is lower in the noise-only image than in the presence of the signal. This is typical behaviour in analog instruments where the presence of signal increases noise level. However, SNR does not take this into account as it is a ratio of two separate measurement. And it makes sense – you would not hear that noise when playing maximum-level signal. However, dynamic range takes this noise increase into account.
Dynamic range
Dynamic range is sometimes used instead of or beside SNR. It is derived in the same way except in this case noise is measured in the presence of signal. Measurement instrument filters the signal out with sharp band-reject filter and measures the noise level. Therefore, dynamic range can be derived from a single measurement.
To continue the FFT examples, below is an FFT with -60 dBV signal (widely used level in dynamic range measurements).
Small signal is used so that it does not generate distortion components or raise the noise floor too much. Dynamic range should give (almost) the same value as SNR.
Some digital devices may mute outputs completely when signal is not present. In that case SNR would look too good when measured the typical way as a ratio of two separate measurements. Measuring noise in the presence of signal, or dynamic range, prevents this.
References
- Wikipedia: Signal-to-noise ratio
- Audio Precision: Signal-to-noise Ratio (SNR), Dynamic Range, and Noise
- Wikipedia: White noise
- Audio Precision: FFT scaling for noise